16. Modern Molecular NNs#
We have seen two chapters about equivariances in Input Data & Equivariances and Equivariant Neural Networks. We have seen one chapter on dealing with molecules as objects with permutation equivariance Graph Neural Networks. We will combine these ideas and create neural networks that can treat arbitrary molecules with point clouds and permutation equivariance. We already saw SchNet is able to do this by working with an invariant point cloud representation (distance to atoms), but modern networks mix in ideas from Equivariant Neural Networks along with graph neural networks (GNN). This is a highly-active research area, especially for predicting energies, forces, and relaxed structures of molecules.
Audience & Objectives
This chapter assumes you have read Input Data & Equivariances, Equivariant Neural Networks, and Graph Neural Networks. You should be able to
Categorize a task (features/labels) by equivariance
Understand body-ordered expansions
Differentiate models based on their message passing, message type, and body-ordering
Warning
This chapter is in progress
16.1. Running This Notebook#
Click the above to launch this page as an interactive Google Colab. See details below on installing packages.
Tip
To install packages, execute this code in a new cell.
!pip install dmol-book
If you find install problems, you can get the latest working versions of packages used in this book here
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
import pandas as pd
import rdkit, rdkit.Chem, rdkit.Chem.rdDepictor, rdkit.Chem.Draw
import networkx as nx
import dmol
my_elements = {6: "C", 8: "O", 1: "H"}
16. Expressiveness#
The Equivariant SO(3) ideas from Equivariant Neural Networks will not work on variable sized molecules because the layers are not permutation equivariant. We also know that graph neural networks (GNNs) have permutation equivariance and, with the correct choice of edge features, rotation and translation invariance. So why go beyond GNNs?
One reason is that the standard GNNs cannot distinguish certain types of graphs relevant for chemistry is they cannot distinguish molecules like decaline and bicylopentyl, which indeed have different properties. Look at the Fig. 16.1 below and think about the degree and neighbors of the atoms near the mixing of the rings – you’ll see if you try to use message passing the two molecules are identical. This is known as the Wesifeiler-Lehman Test [WL68].
Fig. 16.1 Comparison of decaline and bicylopentyl, which have identical output in most GNNs despite being different molecules.#
These can be distinguished if we also have (and use) their Cartesian coordinates. We cannot distinguish enantiomers with GNNs, except maybe with pre-computed node attributes. Even those start to breakdown when we have helical chirality that is not centered at any one atom.
These are arguments for using Cartesian coordinates in addition to a GNN, but why use equivariant neural networks as opposed to the simpler invariant networks discussed in Input Data & Equivariances? Most molnet research is for neural potentials. These are neural networks that predict energy and forces given atom positions and elements. We know that the force on each atom is given by
where \(U\left(\vec{x}\right)\) is the rotation invariant potential given all atom positions \(\vec{r}\). So if we’re predicting a translation, rotation, and permutation invariant potential, why use equivariance? Part of it is performance. Models like SchNet or ANI are invariant and are not as accurate as models like NequiP or TorchMD-NET that have equivariances in their internal layers. Another reason is that there are indeed specific 3D configurations that should have different energies (according to quantum chemistry calculations), but are invariant if treated with pairwise distance alone [PC22].
16.1. The Elements of Modern Molecular NNs#
There has been a flurry of ideas about molents in the last few years, especially with the advances in equivariant neural network layers. Batatia et al.[BBKovacs+22] have proposed a categorization of the main elements of molnets (which they call E(3)-equivariant NNs) that I will adopt here. They categorize the decisions to be made into three parts of the architecture: the atomic cluster expansions (ACE), the body-order of the messages, and the architecture of the message passing neural network (MPNN). This categorization might also be viewed within the GNN theory as node features (ACE), message creation and aggregation (body-order), and node update (MPNN details). See Graph Neural Networks for more details on MPNNs.
This is a relatively new categorization and certainly is not necessary to use. Most papers do not use this categorization and it takes some effort to put models into it. The benefit of thinking about models with this abstractions is it helps us differentiate between the very large number of models now being pursued in the literature. There is also a bit of chaos in teasing out what differentiates the best models from others. For example, it took a while to discover that the most important features in NequIP were data normalization and how atom embeddings are treated [BBKovacs+22]. This categorization is also improving how these models are designed.
16.1.1. Atom features#
Let’s start with the general terminology for an atom. Of course, the input to these networks an atom is just a Cartesian coordinate \(\vec{r}_i\) and the element \(z_i\). As we pass through GNN layers the features will become larger. The atoms are the nodes. The atom features need to be organized a bit differently than previously because some of the features should be invariant with respect to the group — SO(3) — and some need to be equivariant.
16.1.2. Atomic Cluster Expansions#
An ACE is a per-atom tensor. The main idea of ACE is to encode the local environment of an atom into a feature tensor that describes its neighborhood of nearby atoms. This is like distinguishing between an oxygen in an alcohol group vs an oxygen in an ether. Both are oxygens, but we expect them to behave differently. ACE is the same idea, but for nearby atoms in space instead of just on the molecular graph.
The general equation for ACE (assuming O(3) equivariance) is [cite]:
Wow! What an expression. Let’s go through this carefully, starting with the output. \(A^{(t)}_{i, kl_3m_3}\) are the feature tensor values for atom \(i\) at layer \(t\). There are channels indexed by \(k\) and the spherical harmonic indexes \(l_3m_3\). The right-hand side is nearly identical to the G-equivariant neural network layer equation from Equivariant Neural Networks. We have the input
How is this different than a MPNN
To help understand the GCN layer, look at molnet-dframe. It shows an intermediate step of the GCN layer. Each node feature is represented here as a one-hot encoded vector at input. The animation in Fig. 16.2 shows the averaging
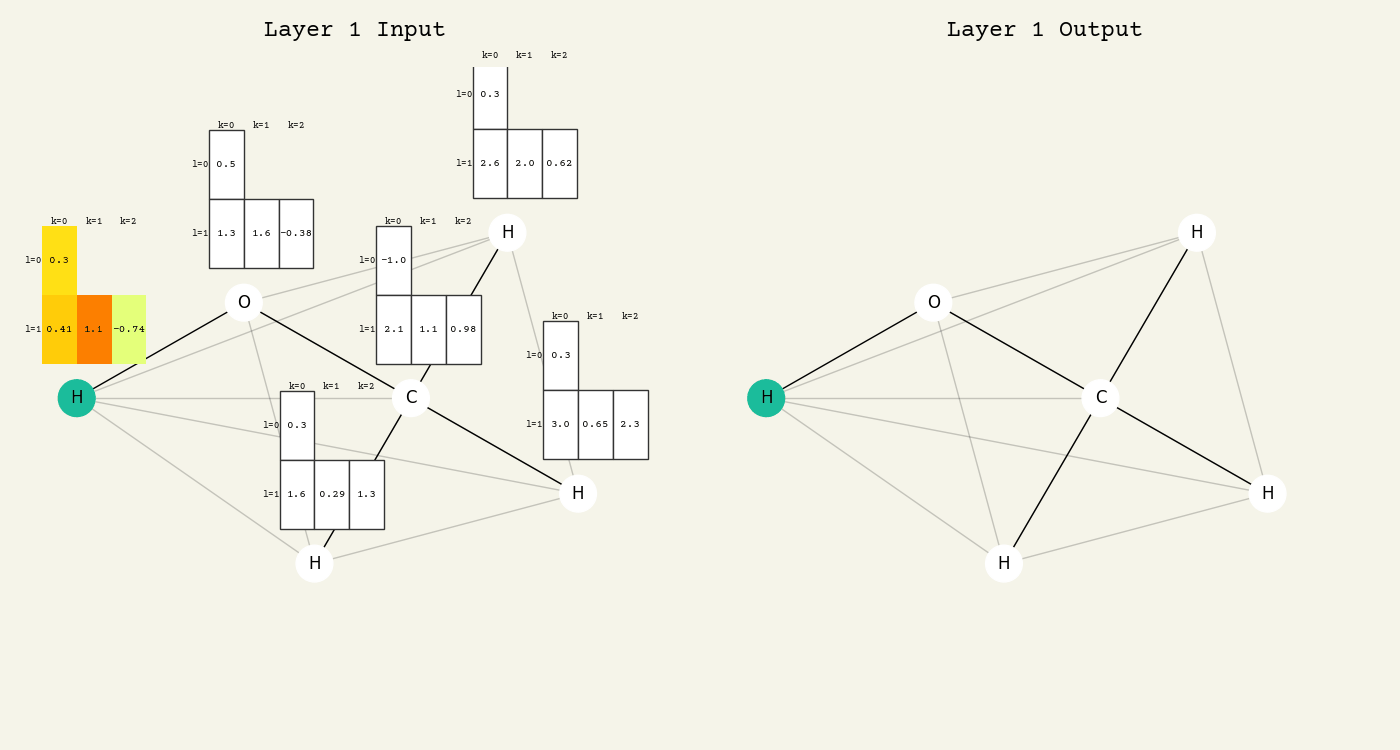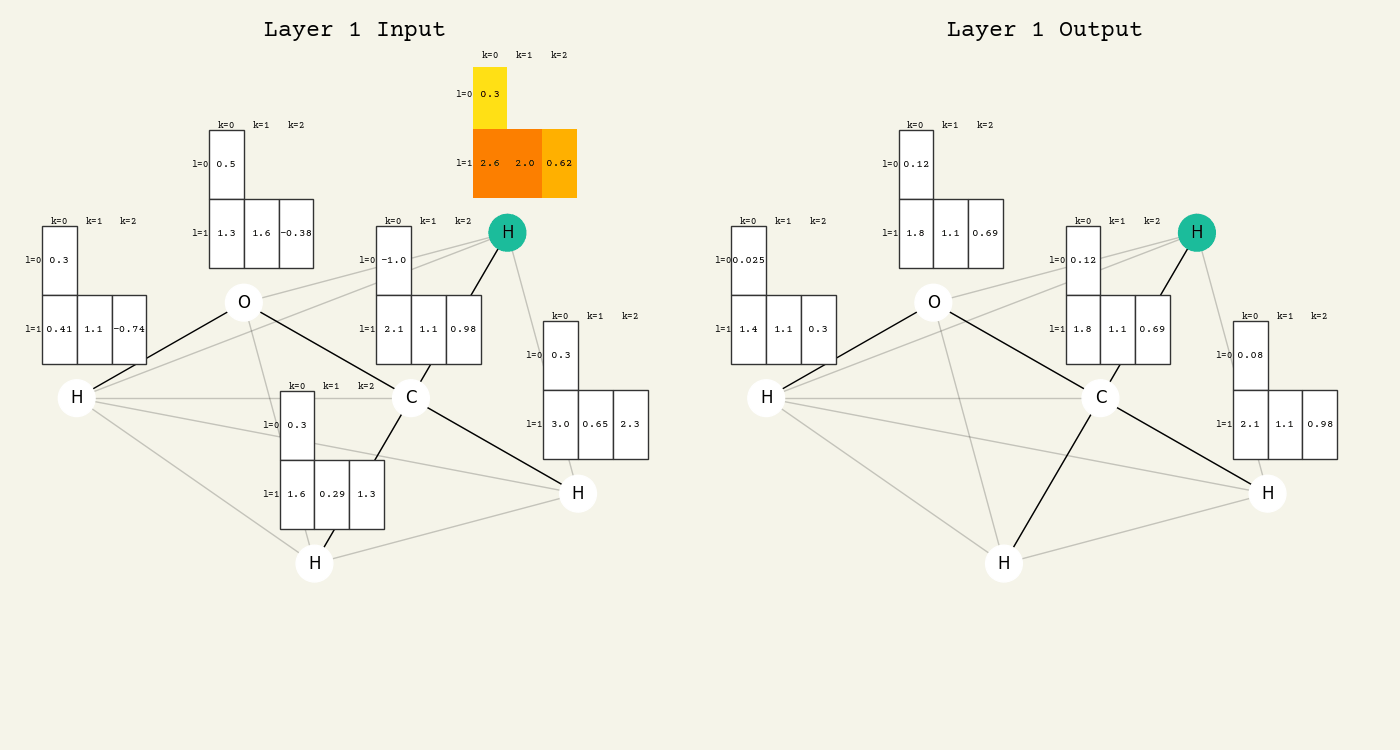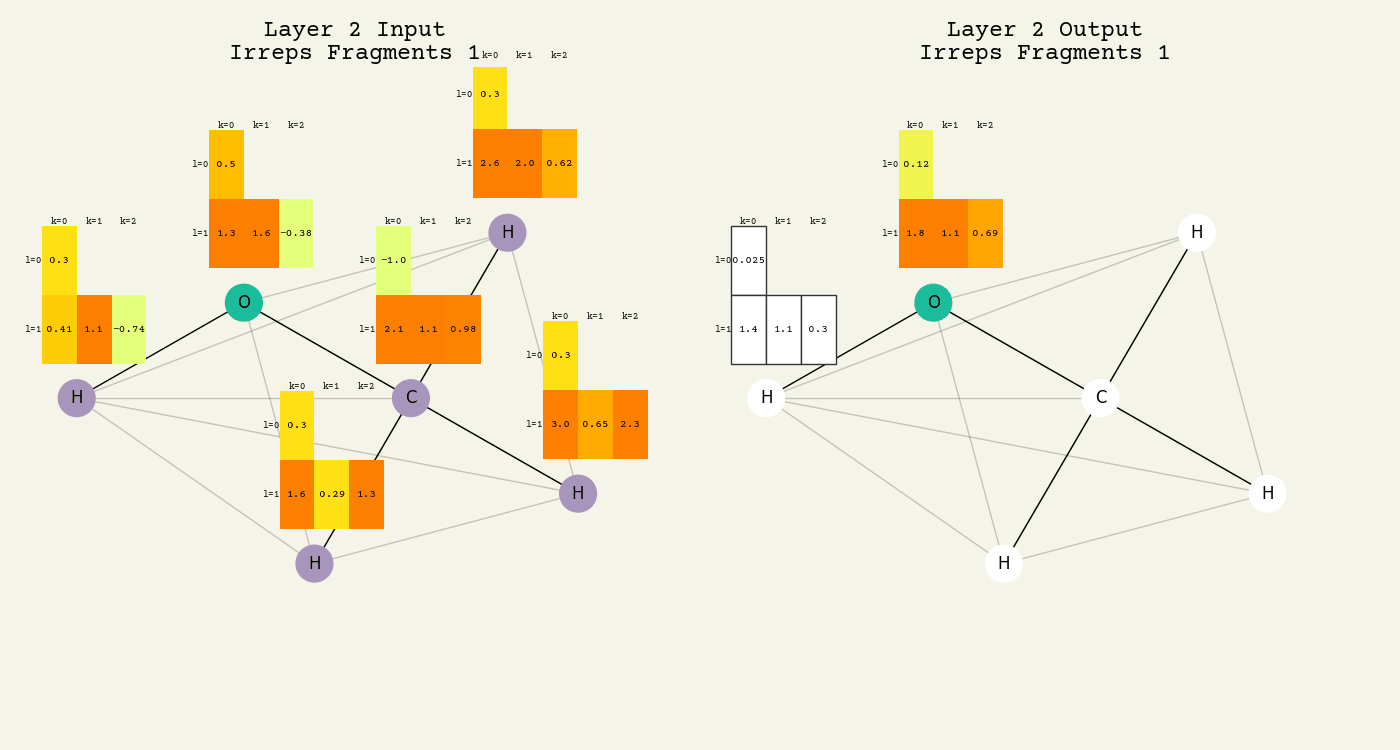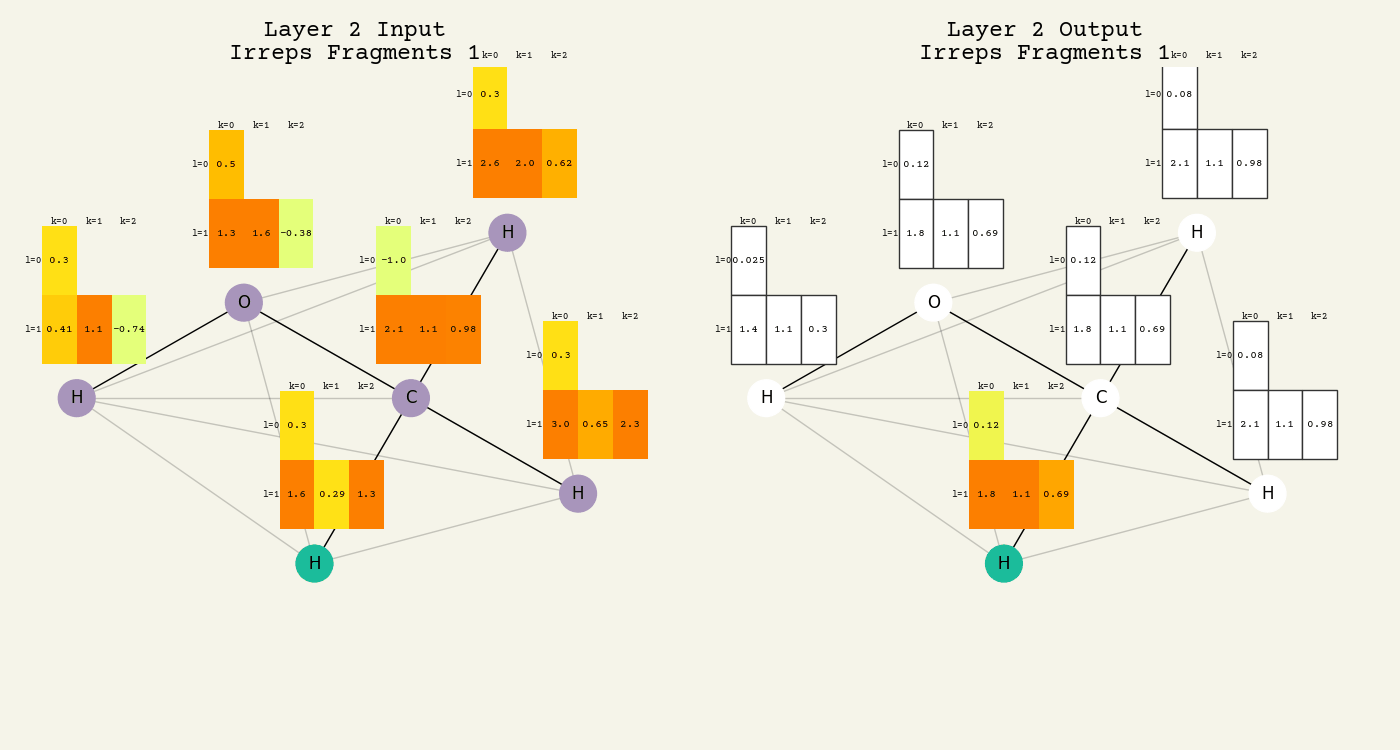
Fig. 16.2 Animation of the graph convolution layer operation. The left is input, right is output node features. Note that two layers are shown (see title change). As the animation plays out, you can see how the information about the atoms propagates through the molecule via the averaging over neighbors. Note how each fragment set is updated independently to maintain equivariance.#
16.2. Normalization#
Physics-based energy/force normalization
Pooling
Layers
16.3. Cited References#
Boris Weisfeiler and Andrei Leman. The reduction of a graph to canonical form and the algebra which appears therein. NTI, Series, 2(9):12–16, 1968.
Sergey N Pozdnyakov and Michele Ceriotti. Incompleteness of graph convolutional neural networks for points clouds in three dimensions. arXiv preprint arXiv:2201.07136, 2022.

